á Pagina precedente Home
page Pagina seguente â
Cap. III. – Problemi non ben posti.
[Sergio Vessella]
N. 1. –
Nozione di problema non ben posto.
1. 1. - Esempio.
·
Supponiamo di conoscere
approssimativamente la legge oraria
del moto rettilineo di un punto, in un intervallo di tempo [0,T] e poniamo la
seguente domanda:
È possibile determinare un’approssimazione
della velocità
del punto stesso?
Se
x = s(t) è l’equazione della legge oraria del moto del punto, è noto che
la sua velocità è data da
v(t)
= s’(t)
Per
eseguirne lo studio, riformuliamo il problema, ponendo il quesito:
Se
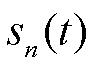è un successione
tale che
(1) 
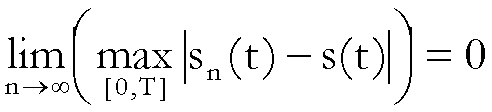
è vero che anche
(2) 
?
·
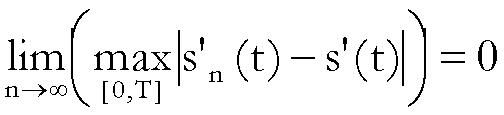La risposta è negativa, come
si deduce dall’esempio già discusso in (V), Cap. II e che qui riformuliamo.
Sia
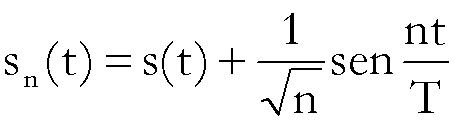, n = 1,2,3,…
,
allora
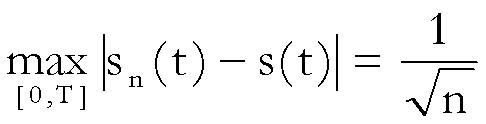, n = 2,3,4,… ,
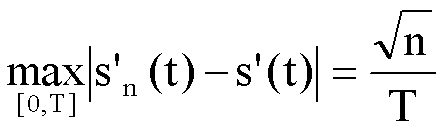, n = 1,2,3,…
quindi la (1) è
verificata, mentre la (2) non è verificata.
·
Diremo brevemente che la
soluzione v non dipende con continuità dal dato s.
N. 2. –
Problemi ben posti secondo Hadamard.
Un possibile schema
a cui possono essere ricondotti molti problemi applicativi è il
seguente:
·
Dati due spazi metrici, (X,d1)
e (Y, d2) e un’applicazione
,
consideriamo il
seguente problema:
(P) Dato
determinare 
tale che
(1) 
.
·
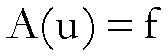In queste ipotesi, il problema P si
dice ben posto secondo Hadamard, se sono verificate le condizioni:
a) per ogni 
esiste una soluzione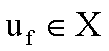 
della (1);
In altre parole: l’applicazione A è
surgettiva;
b) per
ogni 
la (1) ha al più una soluzione;
Ossia
l’applicazione A è anche iniettiva;
c) la
soluzione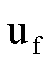 
della (1) dipende con continuità da f.
Cioè:
l’applicazione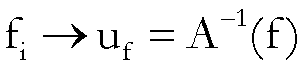 
è
continua da 
in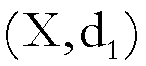 
.
N. 3. -
Definizione generale di problema non ben posto.
·
In generale, un problema si dice non
ben posto se una delle tre condizioni, di cui sopra, a), b), c), non è soddisfatta.
Tra
i vari problemi non ben posti rivestono particolare importanza, per le
applicazioni, quelli per i quali le prime due condizioni, a), b), sono
soddisfatte, mentre la terza c) non è verificata.
Nel
seguito ci occuperemo solo di questi ultimi.
N. 4. –
Problema ben posto secondo Tykhonov.
·
Se X è un insieme e K un suo
sottoinsieme proprio, allora un problema (P)
si dice ben posto secondo Tykhonov se
sono soddisfatte le seguenti condizioni:
a’) è noto a priori che una soluzione u di
(P) esiste ed appartiene a K;
b’) tale soluzione è unica, ossia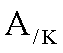 
è iniettivo;
c’) a piccole variazioni di f tali che la
soluzione di (P) appartiene ancora a K, corrispondono piccole variazioni della
soluzione stessa; cioè
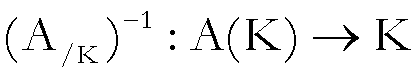è continuo.
4. 1. –
Applicazione.
·
Per illustrare il significato di
questa nozione ritorniamo al problema posto nell’esempio 1.1 e supponiamo che
il punto in movimento abbia un’accelerazione non superiore ad M, cioè
che
(2) 
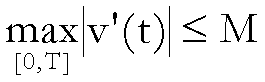
N.B.
Osserviamo, prima
di proseguire, che in questo caso l’applicazione A è definita nel
seguente modo:
,
,
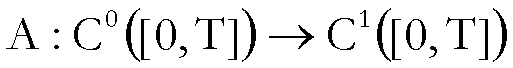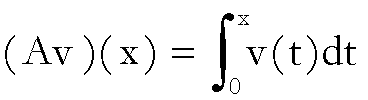e
.
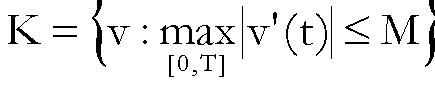Tornando al
precedente ragionamento,
se 
è un’approssimazione
di 
, cioè se
(3) 
,
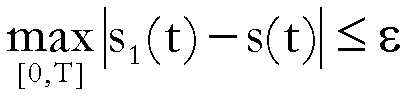dove con 
si è indicato l’errore
di approssimazione, e se 
verifica la relazione (2), allora, posto
,
,
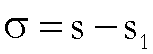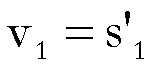e fissato
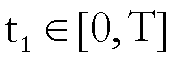
si ha dalla formula
di Taylor con il resto di Lagrange che
per ogni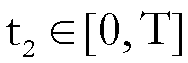 
esiste un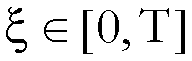 
tale che:
.
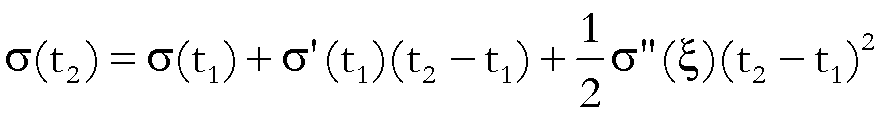Da questa
relazione segue che,
per ogni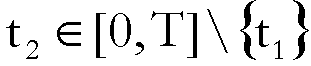 
si ha
.
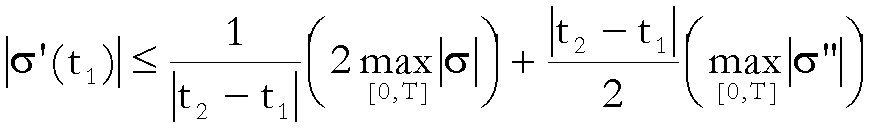Minimizzando la funzione segue:
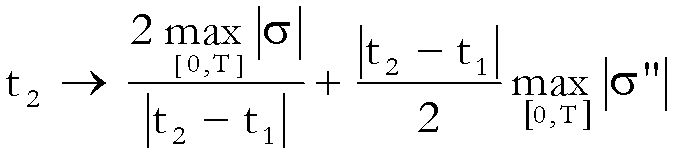
con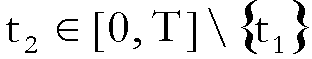 
e poiché da (2) e
(3) segue che
,
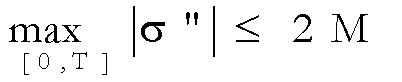
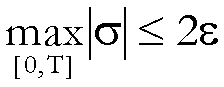si ha
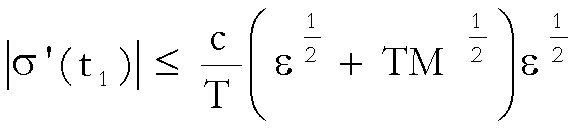
essendo c
una costante indipendente da 
e da 
.
Da questa
relazione segue:
(4) 
·
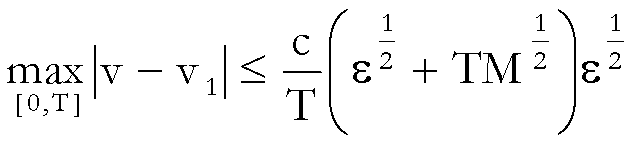
Tale disuguaglianza consente di approssimare
la velocità v con un ordine di approssimazione minore o uguale a 
.
L’introduzione
dell’insieme K, nella nozione di correttezza secondo Tykhnov, equivale all’
introduzione di nuove informazioni nel problema.
Tali informazioni
sono generalmente suggerite dal problema in esame.
Ciò che va
sottolineato è che nella trattazione di un problema non ben posto
non si può fare a meno di esse.
·
Se il problema (P) risulta ben
posto secondo Tykhonov, per un certo insieme K, uno degli aspetti
matematicamente più interessanti consiste nella valutazione del modulo di continuità
dell’applicazione
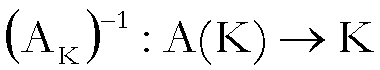
cioè nel valutare
.
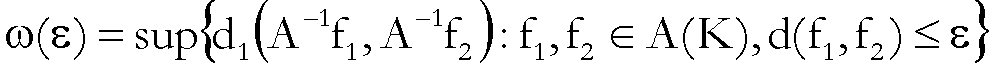[Continua]
á Pagina precedente Home
page Pagina seguente â