Cap. III – a.
[Sergio Vessella]
N. 5. – Equazioni differenziali notevoli.
·
Le osservazioni di Hadamard sui problemi
ben posti sorsero nell’ambito delle equazioni differenziali alle
derivate parziali.
Ricordiamo,
tra le più note, le seguenti:
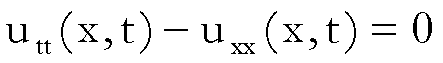 (Equazione delle onde o di
D’Alembert)
(Equazione delle onde o di
D’Alembert)
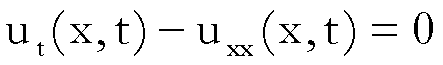 (Equazione del calore o di Fourier)
(Equazione del calore o di Fourier)
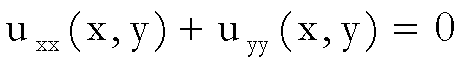 (Equazione del potenziale o di Laplace)
(Equazione del potenziale o di Laplace)
Osservazioni.
Il Lettore che non abbia conoscenze
approfondite di Fisica-Matematica, potrà domandarsi quale sia il significato
fisico di queste equazioni o, in altre parole, in qual modo la necessità di
risolvere alcuni problemi di fisica conduca proprio a queste.
Questo è il compito specifico di un
Fisico-Matematico.
Poiché
l’obiettivo del presente lavoro è quello di illustrare gli studi e il
contributo di Vessella (di carattere soprattutto analitico), non mi soffermerò
sui problemi di fisica che le suddette equazioni risolvono, limitandomi (del
resto, anche per mancanza di spazio), all’aspetto puramente matematico.
Non
solo, ma anche limitatamente alla ricerca di Vessella, non potrò trattenermi
troppo, dato il carattere breve di questo studio, eseguito per l’Annuario
dell’ASMV.
Per
tale ragione, mi limiterò ad esaminare sola la seconda delle tre equazioni
sopra riportate: l’equazione del calore,
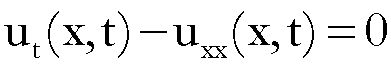
N. 6. –
Equazione del calore.
6.1. - Alcune
premesse.
E’ noto dalla Fisica, a proposito
della conducibilità termica nei corpi solidi, che, riscaldando un
estremo di una sbarra metallica, una certa quantità di calore si propaga
lungo la stessa, per conduzione, mentre un’altra parte si disperde
nell’ambiente, lungo la sbarra, soprattutto per irraggiamento termico.
La funzione che consente il calcolo
di queste temperature non sempre si può determinare facilmente.
Il problema diventa ancora più
complesso se si formulano ipotesi diverse sulle condizioni termiche della sbarra,
specialmente se si voglia determinare la temperatura dei vari punti in funzione
anche del tempo e quindi non in regime stazionario.
Si può dimostrare (v. Petrovskj) che
se 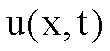 rappresenta la
temperatura della sbarra al tempo t nel punto x, allora u
soddisfa l’equazione
rappresenta la
temperatura della sbarra al tempo t nel punto x, allora u
soddisfa l’equazione
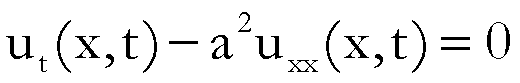
dove a
dipende dalle proprietà termiche della sbarra.
Qui supponiamo
che a sia costante, anzi porremo ![]() .
.
Un esempio
è dato dal problema che segue, che si risolve facendo ricorso all’equazione
del calore, come vedremo fra breve.
6.2.
– Problema.
Poniamo il seguente problema:
vogliamo determinare la temperatura 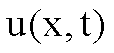 , all’istante t e nel punto x della sbarra, di proprietà
termiche note, sapendo che la temperatura è nulla agli estremi, 0 e 1,
conoscendo la temperatura all’istante T > 0.
, all’istante t e nel punto x della sbarra, di proprietà
termiche note, sapendo che la temperatura è nulla agli estremi, 0 e 1,
conoscendo la temperatura all’istante T > 0.
·
In termini matematici il problema si
può tradurre come segue:
determinare la funzione ![]() , tale che:
, tale che:
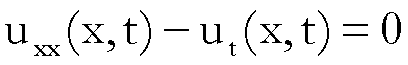 ,
, ![]() ,
, ![]() ,
,
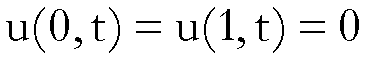 ,
, ![]() ,
,
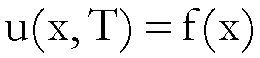 ,
, ![]() ,
,
dove:
·
![]() è un istante noto,
è un istante noto,
·
![]() è una funzione, anch’essa nota, che
rappresenta la distribuzione delle temperature dei punti della sbarra,
all’istante
è una funzione, anch’essa nota, che
rappresenta la distribuzione delle temperature dei punti della sbarra,
all’istante ![]() .
.
Abbiamo, dunque, utilizzato l’equazione
del calore sopra scritta, alla quale abbiamo aggiunto le ipotesi di lavoro.
Il principio di massimo,
valido per l’equazione del calore, assicura che:
(1) 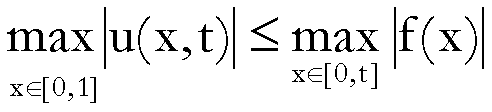 ,
, ![]()
Da questa relazione segue la continuità
dell’applicazione
![]() di
di 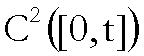 in sé, munito della
distanza
in sé, munito della
distanza ![]() .
.
·
Come conseguenza si ha la
possibilità di prevedere con buona approssimazione la temperatura della
sbarra per ![]() , ossia in istanti successivi a T.
, ossia in istanti successivi a T.
Risulta,
invece, di natura diversa il caso in cui ![]() .
.
·
Si dimostra, infatti, che
per ![]() l’applicazione
l’applicazione 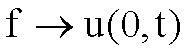 non è continua.
non è continua.
Di conseguenza, in questo caso: il problema
non è ben posto, secondo Hdamard.
Infatti,
per t < T, posto
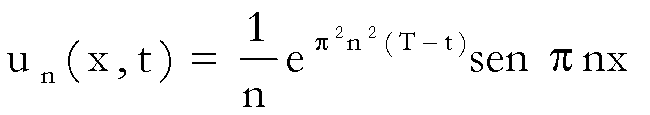 ,
, ![]()
si ha:
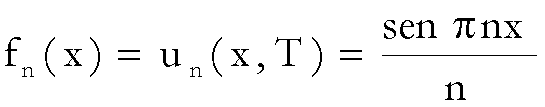 ,
, ![]()
e quindi
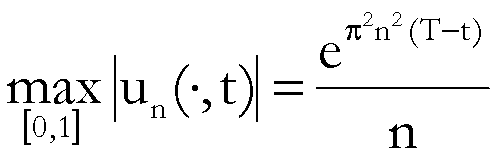
perciò
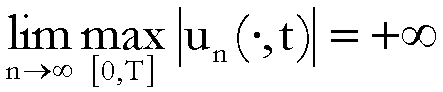
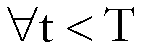
Non è quindi possibile risalire alla
temperatura ![]() in istanti t
precedenti a T.
in istanti t
precedenti a T.
Pertanto, in questo caso, il problema
non è ben posto.
·
Vediamo un possibile approccio allo
studio della stabilità del problema considerato.
Supponiamo
di disporre della seguente limitazione a priori:
(1) 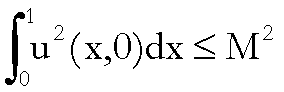
nella
quale ricordiamo che 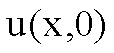 rappresenta la
temperatura all’istante iniziale e che
rappresenta la
temperatura all’istante iniziale e che
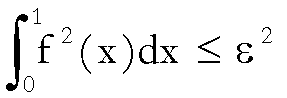 con
con 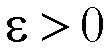
dove ![]() rappresenta l’errore
nell’approssimazione nella distanza
rappresenta l’errore
nell’approssimazione nella distanza
 .
.
Poiché si può provare che la
funzione
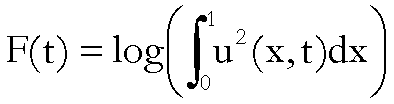
è convessa (v. più avanti),
ne segue
che
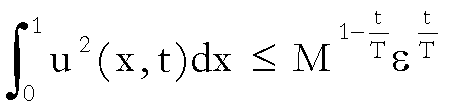 ,
, ![]()
Tale
maggiorazione consente, per la linearità del problema, una valutazione
del modulo di continuità dell’applicazione
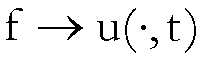 ,
, ![]()
nella metrica
![]() .
.
·
Proviamo, ora, che F è convessa.
Osserviamo
innanzitutto che
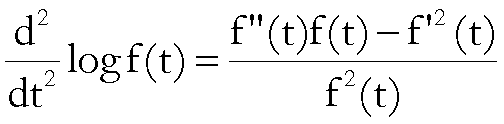
pertanto,
per dimostrare l’assunto basta provare che
(1) 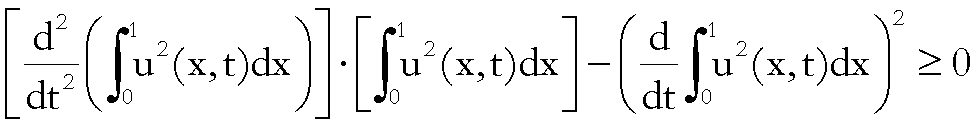 .
.
Ora
(2) 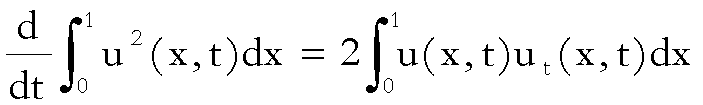
ma
dall’equazione abbiamo che
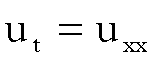
quindi
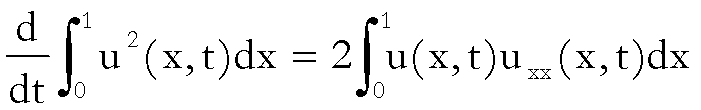 ;
;
integrando
per parti e tenuto conto che
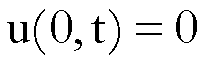 e
e 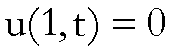
abbiamo
che
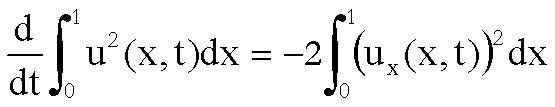
e
derivando ulteriormente abbiamo
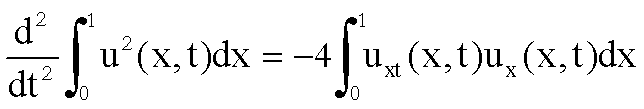 ;
;
da
qui integrando per parti e tenendo conto che le condizioni al bordo
danno
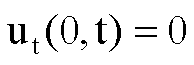 e
e 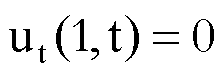
ricaviamo
che
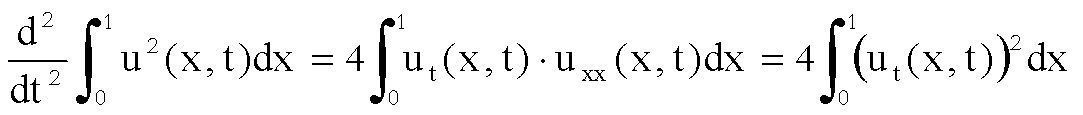 .
.
Nella
seconda uguaglianza abbiamo adoperato l’equazione 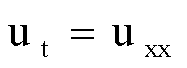 .
.
Dall’ultima
uguaglianza ottenuta e dalla (2) si ha che il membro destro di (1) si scrive:
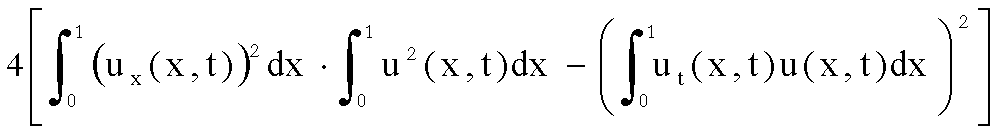 ;
;
e
quest’ultima è non negativa per la disuguaglianza di Cauchy – Schwarz
che qui ricordiamo
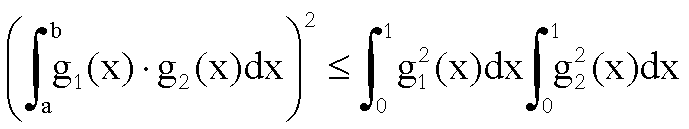 .
.
Pertanto
F è convessa.
·
Quindi per ![]()
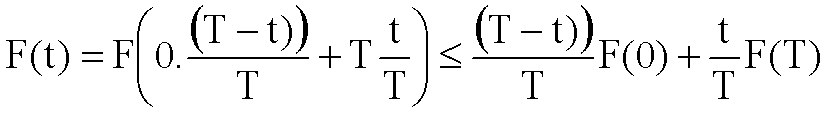
da
cui
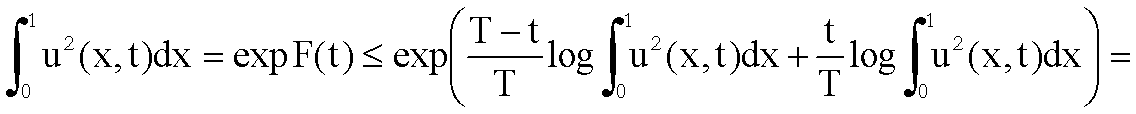
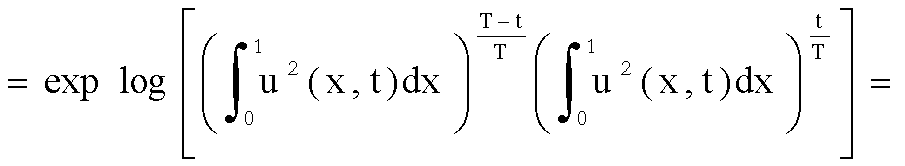
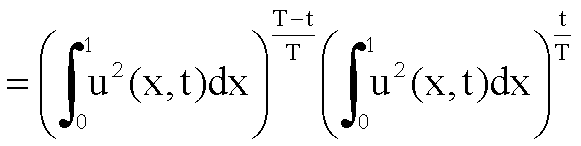 .
.
Nota.
Questa dimostrazione è dovuta a Payne, v.[4].
N. 7. -
Equazione integrale notevole.
Numerosi
problemi applicativi (ad esempio, connessi alla meccanica, alla sismologia,
alla tomografia,…) conducono alla seguente equazione integrale:
(1) 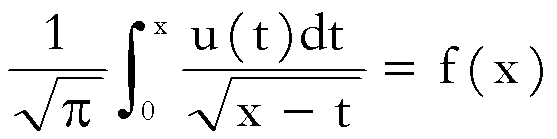
in cui ![]() è assegnata, mentre
è assegnata, mentre ![]() è incognita.
è incognita.
La
(1) deve essere verificata per ogni 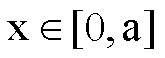 con
con 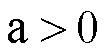 .
.
L’equazione
(1) fu considerata per la prima volta dal matematico norvegese Niels Henrik
Abel (n. 1802 – m. 1829), in relazione ad un problema di meccanica.
Questa
è la prima equazione integrale studiata in matematica.
N. 8. –
Equazione di Abel.
Un altro tipo di equazione di cui la
(1) rappresenta un caso particolare è:
(2) 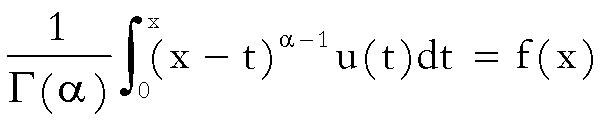
in cui
![]()
e
![]() è una funzione
gamma di Eulero, così definita:
è una funzione
gamma di Eulero, così definita:
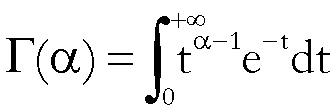 .
.
N. 9. – Altri
problemi non ben posti.
·
Molti problemi che conducono alle
equazioni (1) o (2) risultano essere non ben posti, se l’errore sul dato
f e sull’incognita u è valutato in metriche che non “coinvolgono derivate”.
Tali
sono, ad esempio, le metriche 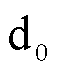 e
e 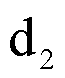 prima introdotte.
prima introdotte.
·
Tra le ragioni del fenomeno di
instabilità ci limitiamo ad accennare a quella che sembra essere la più importante e che chiarisce alcune
ragioni che hanno incoraggiato le ricerche sull’equazione del tipo (2) e sul
seguente operatore:
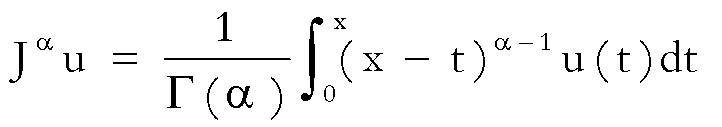 .
.
Sostituiamo,
formalmente, ad a un intero positivo n.
Allora,
poiché
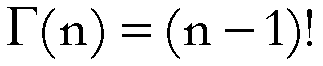
si ha
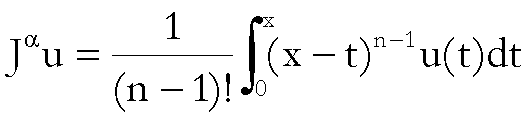
D’altra
parte
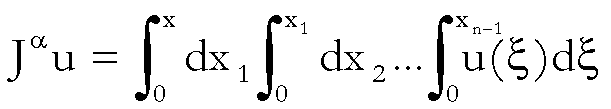
e cioè 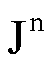 è l’operatore
integrale,
è l’operatore
integrale, ![]() , ripetuto n volte.
, ripetuto n volte.
·
Se consideriamo l’equazione
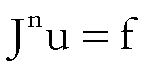
con n intero
positivo, si ha
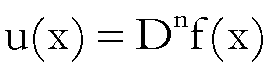 .
.
Come
già ho fatto osservare, l’operazione di derivazione conduce ad un problema
non ben posto.
L’instabilità
dell’inversione di ![]() , con
, con ![]() , sembra proprio dovuta al fatto che
, sembra proprio dovuta al fatto che  si comporta come una
“potenza frazionaria” dell’operatore integrale J e che l’inverso
di
si comporta come una
“potenza frazionaria” dell’operatore integrale J e che l’inverso
di 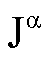 si comporta come una
“derivata frazionaria”.
si comporta come una
“derivata frazionaria”.
L’inverso
di 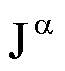 , e quindi la formula risolutiva di (2), è data da:
, e quindi la formula risolutiva di (2), è data da:
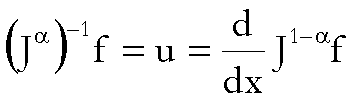
L’operatore
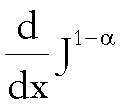 si indica con
si indica con 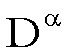
ed è chiamato derivata
frazionaria di ordine 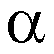 .
.
·
In una monografia (composta insieme
con Gorenflo), Vessella descrive i problemi applicativi connessi
all’equazione di Abel, le proprietà dell’operatore 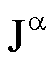 e lo studio della
stabilità relativo alle equazioni del tipo di Abel.
e lo studio della
stabilità relativo alle equazioni del tipo di Abel.
Ma,
almeno per ora, dobbiamo terminare l’esposizione del lavoro matematico di Vessella.
N.
10. - Bibliografia.
[1] Courant R., Hilbert D.: Methods of Mathematical Physics, Interscience
Publisher inc. New York, 1962.
[2] Gorenflo R., Vessella S.: Abel Integral Equation Analysis and
Applications, Lecture Notes in Mathematics, Springer – Verlag, Berlin,
1991.
[3]
Lavrent’ev M.M., Romanov V.G.,
Sisatskij S.P.: Problemi non ben posti in Fisica Matematica
e Analisi, Pubblicazione I.A.G.A., (C.N.R.), quaderno n. 12, Firenze, 1983.
[4] Payne L. E.: Improperly Posed Problems in Partial Differential
Equations, Society for Industrial and Applied Mathematics, 1975.
[5] Petrovkii I. G.: Partial Differential Equations, London Ilife
Books Ltd 1967.
[6]
Pucci. C.
: Discussione del problema di Cauchy per le equazioni di tipo ellittico,
Ann. Mat. Pura e Applicata (IV), Vol. XLVI pp. 131-154.
[7]
Talenti G.:
Sui problemi mal posti, Boll. Un. Mat. Ital. (5) 15-A (1978), 1-29. [FINE]