á Pagina precedente Home
page Pagina seguente â
Cap. II. – Premesse.
[Sergio
Vessella]
N. 1. -
Continuità delle funzioni.
Il
concetto di continuità delle funzioni interviene molto frequentemente,
anche nelle operazioni e nei calcoli più elementari.
Infatti, gran parte delle
operazioni che quotidianamente eseguiamo sono basate su dati ottenuti mediante
misurazioni di lunghezze, aree, volumi, temperature e altro, che non possiamo
mai supporre esatte, ma sempre affette da errori.
Ciò che consente di
trovare risultati con un grado tollerabile di approssimazione, utilizzando
misure approssimate dei dati, sono le proprietà di continuità delle
funzioni che adoperiamo nei nostri calcoli.
1.1. –
Continuità della funzione A(l)
= l 2.
Supponiamo, ad esempio,
di essere interessati alla misura dell’area di un campo di terreno di
forma quadrata.
Sappiamo che, se il lato
del quadrato ha lunghezza l allora la sua area è l 2 .
Quindi, se l =
20,12 m allora, indicando con A l’area del campo, si avrà A =
(20,12)2 m2.
Ora, se ci accontentiamo
di una approssimazione di A, possiamo porre, ad esempio, l1
= 20 m, ottenendo A1= 400 m2.
Dalla teoria, sappiamo
anche che per ottenere approssimazioni più accurate di l 2
dobbiamo far ricorso ad approssimazioni più accurate di l.
·
Cerchiamo di illustrare con maggiori dettagli il
problema ora posto.
Dunque,
consideriamo la funzione A(l) = l 2.
Siano assegnati l0
> 0 ed un altro valore l1 di l.
Supponiamo, inoltre, che l1
differisca da l0, in valore assoluto, di una quantità minore
di un certo numero positivo d, cioè che sia![]()
![]()
(1)
![]() .
.
Allora
(2)
![]() .
.
D’altra parte dalla (1) abbiamo
![]() .
.
Da quest’ultima e dalla
(2) ricaviamo
![]()
e, utilizzando nuovamente la (1), otteniamo
(3) ![]()
In conclusione, abbiamo
dimostrato che,
fissato ![]() ,
,
e posto ![]() , si ha:
, si ha:
![]()
![]()
![]()
In altre parole:
·
la funzione A
= A(l) è continua nel punto l
= l0.
·
OSSERVAZIONI.
Come conseguenza della
continuità della funzione area A(l), e delle altre sopra accennate, potremmo
utilizzare, per il calcolo approssimato, tutti gli strumenti posti a disposizione
dell’Analisi matematica, come, ad esempio il differenziale, che
richiedono sempre condizioni di continuità per le funzioni considerate.
Ma, nei casi più
semplici, come per il calcolo approssimato di un’area, esistono procedimenti di
più facile applicazione, che non richiedono strumenti matematici tanto
complessi.
Ad esempio, se si deve
calcolare l’area A di un tavolo a forma rettangolare con una certa
approssimazione, un teorema di facile uso, consente di stabilire quali devono
essere le approssimazioni delle misure, diciamo x ed y, dei lati.
Il teorema a cui mi
riferisco è il seguente:
·
Se si richiede che il prodotto xy di
due numeri reali, x ed y, risulti approssimato per difetto a meno di 10-n
è necessario assumere, per i fattori x ed y, valori approssimati
a meno di 10-(n+k), essendo k il più piccolo numero
intero verificante la disuguaglianza:
int(x) + int(y) + 2 < 10k.
·
Il teorema prevede anche, inversamente, quale sarà
l’approssimazione del prodotto xy, nell’ipotesi che siano date le
approssimazioni dei fattori x ed y.
Se il calcolo approssimato riguarda funzioni più
complesse, allora conviene ricorrere all’uso dei differenziali.
·
Ad esempio, volendo calcolare, con
approssimazione, la misura dell’ipotenusa z di un triangolo rettangolo,
sapendo che le misure dei cateti sono x = 3,54 e y = 2,13, siamo
condotti a determinare il valore della seguente espressione:
![]()
·
Come si può procedere, senza l’uso della
calcolatrice, e senza eseguire il calcolo direttamente?
Conviene considerare la funzione di due variabili
![]() ,
,
differenziabile nel punto ![]() del suo dominio, ed
applicare la formula:
del suo dominio, ed
applicare la formula:
(***) ![]()
In questa formula:
![]() ;
; ![]() ;
;
![]() ;
; ![]() ;
;
quindi
![]() ;
;
![]() ;
;
Inoltre:
![]()
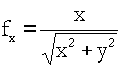 ;
; 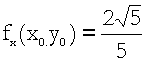 ;
;
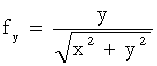 ;
; 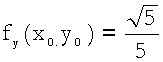 .
.
Applicando, infine, la formula (***), si ha:
![]() @
@![]() =
= 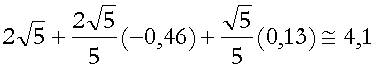 .
.
·
Perché abbiamo scritto una sola cifra decimale nel
risultato?
N. 2. - Problemi di approssimazione.
Rispondiamo ora alle
seguenti domande:
i)
Data la funzione A = A(l), supponiamo che un
certo valore l0 di l sia non maggiore di un numero reale positivo d,
ad esempio ![]() , come deve essere scelto d affinché
, come deve essere scelto d affinché
![]() non superi
non superi ![]() ?
?
ii)
Se non sono noti i valori di ![]() ed
ed ![]() , ma si sa che
, ma si sa che ![]() , essendo d
un numero reale positivo dato, è possibile determinare valori di d
per cui anche
, essendo d
un numero reale positivo dato, è possibile determinare valori di d
per cui anche ![]() sia arbitrariamente
piccola?
sia arbitrariamente
piccola?
·
Per rispondere alla prima domanda, dobbiamo provare
che esistono valori positivi di d per
cui
(*) 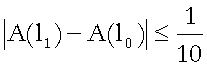
Allo scopo, osserviamo
che la (3), con l’ulteriore ipotesi che ![]() , fornisce le disuguaglianze:
, fornisce le disuguaglianze:
![]()
Infine, i valori positivi
di d per cui
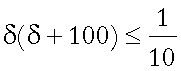
verificano sicuramente la disuguaglianza (*), e quindi
offrono la soluzione al primo quesito.
·
Per quanto riguarda la seconda domanda, la risposta
è negativa.
Vediamo perché.
Dalla disuguaglianza
triangolare e dalla (1), abbiamo
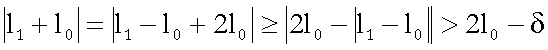
Da quest’ultima e dalla
(2) otteniamo,
se ![]()
(4) ![]()
Può quindi accadere che ![]() superi il numero
arbitrariamente scelto
superi il numero
arbitrariamente scelto
![]()
anche se ![]() .
.
·
Ora, supponiamo che sia
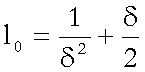 e
e 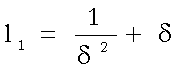 ,
,
allora
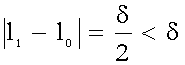
quindi la ![]() è soddisfatta, mentre
dalla (4) si ha
è soddisfatta, mentre
dalla (4) si ha
(5) 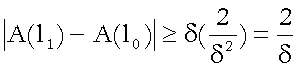 ,
,
da cui se
![]()
anche
![]() ;
;
invece, dalla (5)
![]()
Quindi, pur essendo ![]() non è detto
che la differenza
non è detto
che la differenza ![]() possa assumere
valori arbitrariamente piccoli.
possa assumere
valori arbitrariamente piccoli.
N. 3. – Spazi metrici.
·
Per precisare ulteriormente i concetti illustrati
prima e per preparare il terreno per la discussione successiva, richiamiamo la
definizione di continuità di applicazioni tra spazi metrici.
Allo scopo cominciamo a ricordare
alcune definizioni.
3. 1. - Distanza su un insieme.
·
Sia X un insieme.
Si chiama distanza su
X un’applicazione
![]() R
R ![]()
godente delle seguenti proprietà:
a) ![]()
![]()
b) ![]()
![]()
c) ![]()
![]()
d) ![]()
![]()
·
Esempi di distanze su un insieme.
a) Se ![]() R
R
allora
![]()
è una distanza su R;
b) Se ![]() R2
R2
allora
![]()
![]()
sono distanze su R2.
g) Se X è un insieme qualsiasi,
allora
![]()
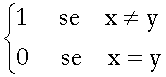
è una distanza su X.
Lascio al Lettore la facile verifica.
3. 2. - Spazio metrico.
·
Un insieme X con una distanza d, definita su
di esso, si chiama spazio metrico.
Sia chiaro, dunque, che uno
spazio metrico è una coppia (X,d) costituita da un insieme X e una
distanza d definita in esso.
In pratica, dato
l’insieme X, quando dal contesto è chiaro quale sia la distanza definita su di
esso, si dice semplicemente che X è uno spazio metrico.
·
Esempi di spazi
metrici, utili per il seguito.
1) Siano a e b due numeri
reali con a < b e sia
![]() ,
,
essendo
![]()
·
Ebbene, è possibile verificare che, posto:
![]() ,
,
l’applicazione
![]()
essendo
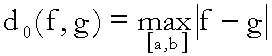 ,
,
![]()
soddisfa alle quattro proprietà della distanza e
che, quindi, la coppia
![]()
è uno spazio metrico.
Omettiamo la
dimostrazione, per brevità.
2) Sia ![]() un numero intero e
sia
un numero intero e
sia
![]()
allora, posto
![]() ,
,
si dimostra che ![]() è ancora una distanza
su
è ancora una distanza
su ![]()
e che tale è anche la ![]() definita da
definita da
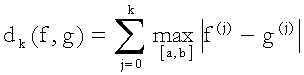
Anche ora, dobbiamo
rinunciare alla dimostrazione, per brevità.
·
Riportiamo, ora, la definizione di
continuità di un’applicazione fra due spazi metrici. [Continua]
á Pagina precedente Home page Pagina seguente â