á Pagina precedente Home page Pagina seguente â

Cap. II – a.

[Sergio Vessella]

N. 4. - Continuità di un’applicazione tra spazi metrici.

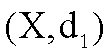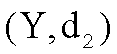Siano e due spazi metrici e

un’applicazione da X ad Y.

· Si dice che F è continua nel punto 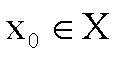se avviene che

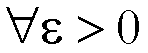
tale che

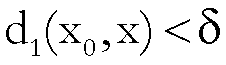
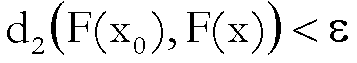
· Inoltre la F si dice continua in X se è continua in ogni punto .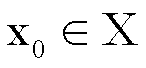

Si osservi che la continuità di un’applicazione dipende dalle distanze che sono poste in X ed Y.

Si osservi ancora che, curiosamente, se X è un qualsiasi insieme non vuoto e 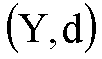è un qualsiasi spazio metrico, allora, considerando in X la distanza 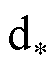definita nell’esempio g (v. sopra), una qualsiasi applicazione

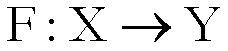
risulta continua in X.

· Per la dimostrazione, osserviamo che, se 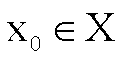è un arbitrario punto di X allora

,

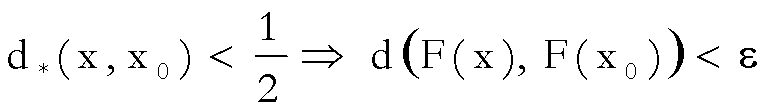
perché se 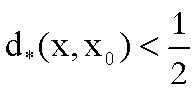allora dalla definizione di 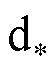segue che 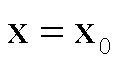e quindi

.

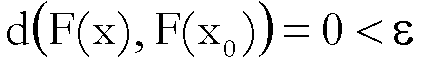4. 1. - Esempi di continuità.

Come primo esempio, consideriamo l’applicazione

(1)

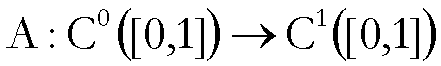
(2)

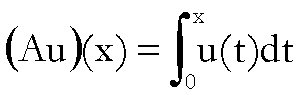
Su 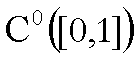e 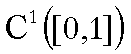consideriamo la stessa distanza:

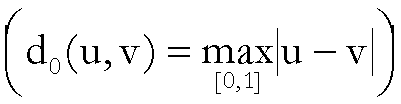
· Ciò posto, vogliamo dimostrare che

(I) l’applicazione è continua;

(II) 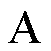non è suriettiva;

(III) 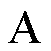è iniettiva.

· Dimostriamo la (I).

Se 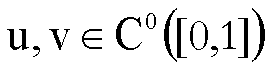allora

=

;

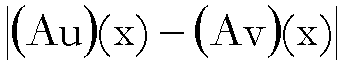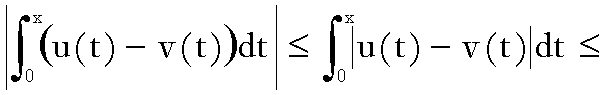
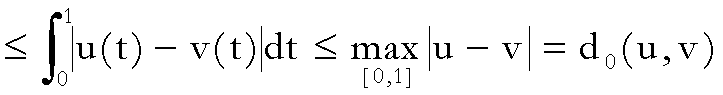quindi

.

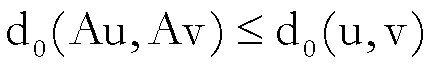Da questa relazione e dalla definizione, segue la continuità di .

· Dimostriamo la (II).

Poiché

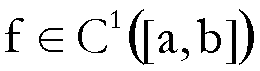ed ,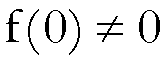

ne segue che non esiste alcuna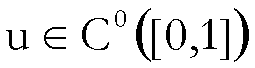

tale che

.

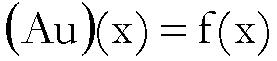Questo accade perché

.

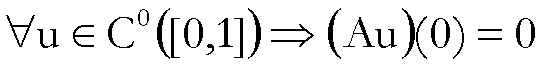· Dimostriamo la (III).

Siano, ora,

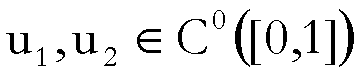
tali che

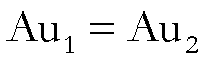
allora

,

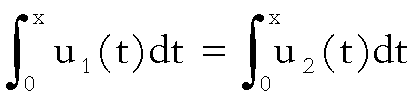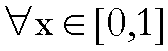
Pertanto, applicando il teorema fondamentale del calcolo, abbiamo che

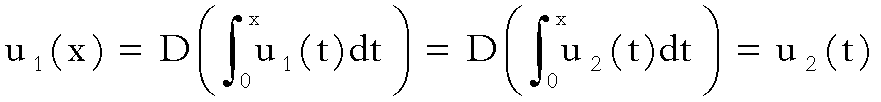
ossia, in definitiva:

.

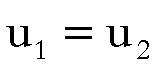4. 2. - Altri due teoremi importanti: (IV) e (V).

· Considerando e il suo sottoinsieme 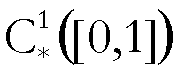, così definito:

,

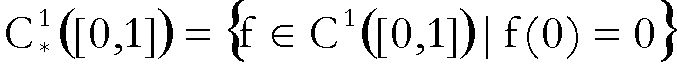si può dimostrare che:

(IV) .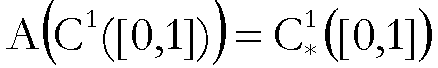

Infatti, come abbiamo osservato prima,

;

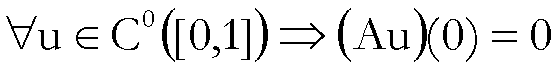inoltre .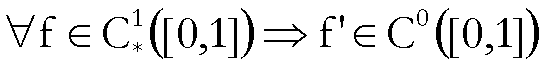

Di conseguenza:

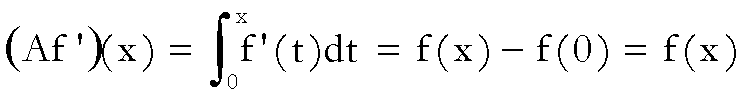
ossia

.

· Infine, dimostriamo che

(V) L’applicazione inversa di A:

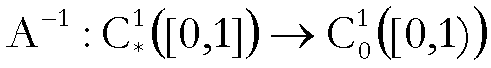
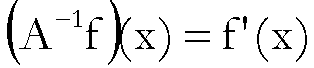
non è continua.

Infatti, se

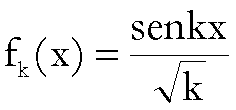
è una successione di funzioni di ,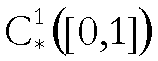

allora

.

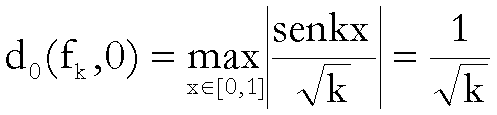
Ora, se l’applicazione 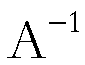fosse continua,

poiché

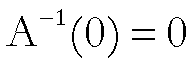
dovrebbe verificarsi che

(**) .

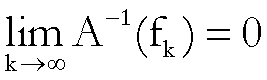Ma ciò non accade, perché

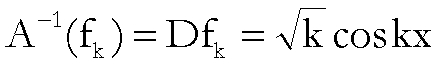
e

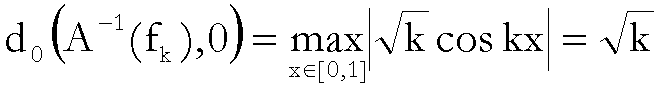
e quindi la relazione (**) non è vera. [Continua]

á Pagina precedente Home page Pagina seguente â